Fit model to data¶
We will fit a Polyclonal model to the RBD antibody mix we simulated.
First, we read in that simulated data. Recall that we simulated both “exact” and “noisy” data, with several average per-library mutations rates, and at six different concentrations. Here we analyze the noisy data for the library with an average of 3 mutations per gene, measured at three different concentrations, as this represents a fairly realistic representation of a real experiment:
[1]:
import requests
import tempfile
import pandas as pd
import polyclonal
noisy_data = (
pd.read_csv("RBD_variants_escape_noisy.csv", na_filter=None)
.query('library == "avg3muts"')
.query("concentration in [0.25, 1, 4]")
.reset_index(drop=True)
)
noisy_data
[1]:
| library | barcode | concentration | prob_escape | aa_substitutions | IC90 | |
|---|---|---|---|---|---|---|
| 0 | avg3muts | AAAACTGCTGAGGAGA | 0.25 | 0.054700 | 0.08212 | |
| 1 | avg3muts | AAAAGCAGGCTACTCT | 0.25 | 0.000000 | 0.08212 | |
| 2 | avg3muts | AAAAGCTATAGGTGCC | 0.25 | 0.007613 | 0.08212 | |
| 3 | avg3muts | AAAAGGTATTAGTGGC | 0.25 | 0.001363 | 0.08212 | |
| 4 | avg3muts | AAAAGTGCCTTCGTTA | 0.25 | 0.000000 | 0.08212 | |
| ... | ... | ... | ... | ... | ... | ... |
| 119995 | avg3muts | GAGCATGATCGACGAA | 1.00 | 0.000000 | Y508V H519I | 0.10830 |
| 119996 | avg3muts | GAGCATGATCGACGAA | 4.00 | 0.000000 | Y508V H519I | 0.10830 |
| 119997 | avg3muts | CTTAAAATAGCTGGTC | 0.25 | 0.000000 | Y508W | 0.08212 |
| 119998 | avg3muts | CTTAAAATAGCTGGTC | 1.00 | 0.012260 | Y508W | 0.08212 |
| 119999 | avg3muts | CTTAAAATAGCTGGTC | 4.00 | 0.000000 | Y508W | 0.08212 |
120000 rows × 6 columns
For spatial regularization (encouraging epitopes to be structurall proximal residues), we read the inter-residue distances in angstroms from PDB 6m0j:
[2]:
# we read the PDB from the webpage into a temporary file and get the distances from that.
# you could also just download the file manually and then read from it.
r = requests.get("https://files.rcsb.org/download/6XM4.pdb")
with tempfile.NamedTemporaryFile() as tmpf:
_ = tmpf.write(r.content)
tmpf.flush()
spatial_distances = polyclonal.pdb_utils.inter_residue_distances(tmpf.name, ["A"])
spatial_distances
[2]:
| site_1 | site_2 | distance | chain_1 | chain_2 | |
|---|---|---|---|---|---|
| 0 | 27 | 28 | 1.332629 | A | A |
| 1 | 27 | 29 | 4.612508 | A | A |
| 2 | 27 | 30 | 8.219518 | A | A |
| 3 | 27 | 31 | 11.016782 | A | A |
| 4 | 27 | 32 | 13.087037 | A | A |
| ... | ... | ... | ... | ... | ... |
| 548623 | 1308 | 1310 | 30.826773 | A | A |
| 548624 | 1308 | 1311 | 75.350853 | A | A |
| 548625 | 1309 | 1310 | 12.374796 | A | A |
| 548626 | 1309 | 1311 | 115.681534 | A | A |
| 548627 | 1310 | 1311 | 106.112328 | A | A |
548628 rows × 5 columns
Initialize a Polyclonal model with these data, including three epitopes. We know from prior work the three most important epitopes and a key mutation in each, so we use this prior knowledge to “seed” initial guesses that assign large escape values to a key site in each epitope:
site 417 for class 1 epitope, which is often the least important
site 484 for class 2 epitope, which is often the dominant one
site 444 for class 3 epitope, which is often the second most dominant one
[3]:
poly_abs = polyclonal.Polyclonal(
data_to_fit=noisy_data,
activity_wt_df=pd.DataFrame.from_records(
[
("1", 1.0),
("2", 3.0),
("3", 2.0),
],
columns=["epitope", "activity"],
),
site_escape_df=pd.DataFrame.from_records(
[
("1", 417, 10.0),
("2", 484, 10.0),
("3", 444, 10.0),
],
columns=["epitope", "site", "escape"],
),
data_mut_escape_overlap="fill_to_data",
spatial_distances=spatial_distances,
)
Now fit the Polyclonal model, logging output every 100 steps. Note how the fitting first just fits a site level model to estimate the average effects of mutations at each site, and then fits the full model. Here we fix the Hill coefficient at one and the non-neutralized fraction at zero:
[4]:
# NBVAL_IGNORE_OUTPUT
opt_res = poly_abs.fit(
logfreq=200,
reg_escape_weight=0.01,
reg_spatial2_weight=1e-5,
reg_uniqueness2_weight=0,
fix_non_neutralized_frac=True,
fix_hill_coefficient=True,
)
#
# Fitting site-level model.
# Starting optimization of 522 parameters at Tue Apr 4 16:01:08 2023.
step time_sec loss fit_loss reg_escape reg_spread reg_spatial reg_uniqueness reg_uniqueness2 reg_activity reg_hill_coefficient reg_non_neutralized_frac
0 0.10483 2991.9 2980.2 0.29701 0 0 0 0 11.418 0 0
200 24.563 1876 1836.9 2.3802 0 25.111 0 0 11.569 0 0
308 37.745 1873.6 1835.4 2.3448 0 24.241 0 0 11.592 0 0
# Successfully finished at Tue Apr 4 16:01:45 2023.
#
# Fitting model.
# Starting optimization of 5799 parameters at Tue Apr 4 16:01:45 2023.
step time_sec loss fit_loss reg_escape reg_spread reg_spatial reg_uniqueness reg_uniqueness2 reg_activity reg_hill_coefficient reg_non_neutralized_frac
0 0.13785 2026.1 1960.5 29.725 3.6371e-30 24.241 0 0 11.592 0 0
200 31.743 492.84 378.86 33.574 20.624 46.484 0 0 13.3 0 0
400 62.818 479.16 366.6 32.471 21.461 45.134 0 0 13.489 0 0
600 93.955 476.55 364.79 31.686 22.005 44.596 0 0 13.467 0 0
800 124.81 469.69 358.68 31.313 22.319 43.888 0 0 13.489 0 0
1000 155.41 466.36 356.22 31.011 22.471 43.178 0 0 13.479 0 0
1200 186.12 462.73 353.63 30.727 22.423 42.489 0 0 13.454 0 0
1400 216.23 462.18 352.96 30.669 22.483 42.602 0 0 13.464 0 0
1600 246.06 457.12 347.99 30.439 22.776 42.496 0 0 13.421 0 0
1800 275.75 456.23 347.31 30.348 22.746 42.382 0 0 13.447 0 0
1826 279.48 456.23 347.31 30.345 22.75 42.375 0 0 13.449 0 0
# Successfully finished at Tue Apr 4 16:06:25 2023.
We can now visualize the resulting curve fits and activity values and compare them to the “true” activity values used to simulate the data. Note that the Hill coefficients are one and the non-neutralized fractions are zero because we fixed them as such above:
[5]:
poly_abs.curve_specs_df.round(1)
[5]:
| epitope | activity | hill_coefficient | non_neutralized_frac | |
|---|---|---|---|---|
| 0 | 1 | 1.5 | 1.0 | 0.0 |
| 1 | 2 | 3.2 | 1.0 | 0.0 |
| 2 | 3 | 2.4 | 1.0 | 0.0 |
[6]:
# NBVAL_IGNORE_OUTPUT
poly_abs.curves_plot()
[6]:
[7]:
# NBVAL_IGNORE_OUTPUT
poly_abs.activity_wt_barplot()
[7]:
[8]:
# NBVAL_IGNORE_OUTPUT
import altair as alt
true_activities = pd.read_csv("RBD_activity_wt_df.csv")
activity_wt_comparison = (
pd.concat(
[
poly_abs.activity_wt_df.rename(columns={"activity": "predicted"}),
true_activities.rename(columns={"activity": "actual"}).drop(
columns="epitope"
),
],
axis=1,
)
).melt(
id_vars=["epitope"],
value_vars=["actual", "predicted"],
var_name="value_type",
value_name="wildtype activity",
)
alt.Chart(activity_wt_comparison).mark_bar(size=35).encode(
x="value_type:O",
y="wildtype activity:Q",
color=alt.Color(
"epitope:N", scale=alt.Scale(range=list(poly_abs.epitope_colors.values()))
),
column="epitope:N",
tooltip=["value_type", alt.Tooltip("wildtype activity", format=".3f"), "epitope"],
).properties(width=100, height=125)
[8]:
Similarly, we can visualize the resulting fits for the escape values, and compare them to the “true” escape values used to simulate the data. Note how entries can be filtered by how many variants a mutation is seen in (times_seen):
[9]:
# NBVAL_IGNORE_OUTPUT
poly_abs.mut_escape_plot()
[9]:
For these simulated data, we can also see how well the fit model does on the “true” simulated values from a library with a different (higher) mutation rate. We therefore read in the “exact” simulated data from a library with a different mutation rate:
[10]:
exact_data = (
pd.read_csv("RBD_variants_escape_exact.csv", na_filter=None)
.query('library == "avg3muts"')
.query("concentration in [0.25, 1, 0.5]")
.reset_index(drop=True)
)
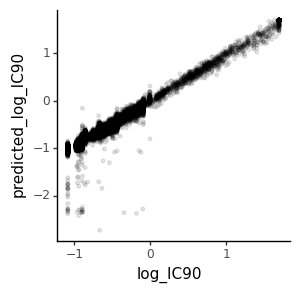
We will compare the true simulated IC90 values to those predicted by the fit model. We make the comparison on a log scale, and clip IC90s at values >50 as likely to be way outside the dynamic range given the concentrations used:
[11]:
# NBVAL_IGNORE_OUTPUT
import numpy
from plotnine import *
max_ic90 = 50
# we only need the variants, not the concentration for the IC90 comparison
ic90s = (
exact_data[["aa_substitutions", "IC90"]]
.assign(IC90=lambda x: x["IC90"].clip(upper=max_ic90))
.drop_duplicates()
)
ic90s = poly_abs.icXX(ic90s, x=0.9, col="predicted_IC90", max_c=max_ic90)
ic90s = ic90s.assign(
log_IC90=lambda x: numpy.log10(x["IC90"]),
predicted_log_IC90=lambda x: numpy.log10(x["predicted_IC90"]),
)
corr = ic90s["log_IC90"].corr(ic90s["predicted_log_IC90"]) ** 2
print(f"Correlation (R^2) is {corr:.2f}")
ic90_corr_plot = (
ggplot(ic90s)
+ aes("log_IC90", "predicted_log_IC90")
+ geom_point(alpha=0.1, size=1)
+ theme_classic()
+ theme(figure_size=(3, 3))
)
_ = ic90_corr_plot.draw()
# ic90_corr_plot.save('IC90_pred_vs_actual.pdf', height=3.5, width=3.5)
Correlation (R^2) is 0.97
Next we see how well the model predicts the variant-level escape probabilities \(p_v\left(c\right)\), by reading in exact data from the simulations, and then making predictions of escape probabilities. We both examine and plot the correlations:
[12]:
# NBVAL_IGNORE_OUTPUT
exact_vs_pred = poly_abs.prob_escape(variants_df=exact_data)
print(f"Correlations (R^2) at each concentration:")
display(
exact_vs_pred.groupby("concentration")
.apply(lambda x: x["prob_escape"].corr(x["predicted_prob_escape"]) ** 2)
.rename("correlation (R^2)")
.reset_index()
.round(2)
)
pv_corr_plot = (
ggplot(exact_vs_pred)
+ aes("prob_escape", "predicted_prob_escape")
+ geom_point(alpha=0.1, size=1)
+ facet_wrap("~ concentration", nrow=1)
+ theme_classic()
+ theme(figure_size=(3 * exact_vs_pred["concentration"].nunique(), 3))
)
_ = pv_corr_plot.draw()
Correlations (R^2) at each concentration:
| concentration | correlation (R^2) | |
|---|---|---|
| 0 | 0.25 | 0.99 |
| 1 | 0.50 | 1.00 |
| 2 | 1.00 | 1.00 |
We also examine the correlation between the “true” and inferred mutation-escape values, \(\beta_{m,e}\). In general, it’s necessary to ensure the epitopes match up for this type of comparison as it is arbitrary which epitope in the model is given which name. But above we seeded the epitopes at the site level using site_effects_df when we initialized the Polyclonal object, so they match up with class 1, 2, and 3:
[13]:
# NBVAL_IGNORE_OUTPUT
import altair as alt
mut_escape_pred = pd.read_csv("RBD_mut_escape_df.csv").merge(
(
poly_abs.mut_escape_df.assign(
epitope=lambda x: "class " + x["epitope"].astype(str)
).rename(columns={"escape": "predicted escape"})
),
on=["mutation", "epitope"],
validate="one_to_one",
)
print("Correlation (R^2) between predicted and true values:")
corr = (
mut_escape_pred.groupby("epitope")
.apply(lambda x: x["escape"].corr(x["predicted escape"]) ** 2)
.rename("correlation (R^2)")
.reset_index()
)
display(corr.round(2))
# for testing since we nbval ignore cell output
assert (
numpy.allclose(
corr["correlation (R^2)"], numpy.array([0.60, 0.96, 0.95]), atol=0.02
)
== True
)
corr_chart = (
alt.Chart(mut_escape_pred)
.encode(
x="escape",
y="predicted escape",
color=alt.Color(
"epitope", scale=alt.Scale(range=list(poly_abs.epitope_colors.values()))
),
tooltip=["mutation", "epitope"],
)
.mark_point(opacity=0.5)
.properties(width=250, height=250)
.facet(column="epitope")
.resolve_scale(
x="independent",
y="independent",
)
)
corr_chart
Correlation (R^2) between predicted and true values:
| epitope | correlation (R^2) | |
|---|---|---|
| 0 | class 1 | 0.60 |
| 1 | class 2 | 0.96 |
| 2 | class 3 | 0.95 |
[13]:
The correlations are strongest for the dominant epitope (class 2), which makes sense as this will drive the highest escape signal.
