ispline

Implements Isplines, which are monotonic spline functions that are defined in terms of Msplines. Also implements Isplines_total for the weighted sum of a Isplines family.

See Ramsay (1988) for details about these splines, and also note the corrections in the Praat manual to the errors in the I-spline formula by Ramsay (1988).

class dms_variants.ispline.Isplines(order, mesh, x)

Bases: object

Implements I-splines (see Ramsay (1988)).

Parameters:

• order (int) – Sets Isplines.order.

• mesh (array-like) – Sets Isplines.mesh.

• x (numpy.ndarray) – Sets Isplines.x.

order

Order of spline, \(k\) in notation of Ramsay (1988). Note that the degree of the I-spline is equal to \(k\), while the associated M-spline has order \(k\) but degree \(k - 1\).

Type:

int

mesh

Mesh sequence, \(\xi_1 < \ldots < \xi_q\) in the notation of Ramsay (1988). This class implements fixed mesh sequences.

Type:

numpy.ndarray

n

Number of members in spline, denoted as \(n\) in Ramsay (1988). Related to number of points \(q\) in the mesh and the order \(k\) by \(n = q - 2 + k\).

Type:

int

lower

Lower end of interval spanned by the splines (first point in mesh).

Type:

float

upper

Upper end of interval spanned by the splines (last point in mesh).

Type:

float

Note

The methods of this class cache their results and return immutable numpy arrays. Do not make these arrays mutable and change their values, as this will lead to invalid caching.

Example

Short examples to demonstrate and test Isplines:

>>> import itertools
>>> import numpy
>>> import pandas as pd
>>> import scipy.optimize
>>> from dms_variants.ispline import Isplines

>>> order = 3
>>> mesh = [0.0, 0.3, 0.5, 0.6, 1.0]
>>> x = numpy.array([0, 0.2, 0.3, 0.4, 0.8, 0.99999])
>>> isplines = Isplines(order, mesh, x)
>>> isplines.order
3
>>> isplines.mesh
array([0. , 0.3, 0.5, 0.6, 1. ])
>>> isplines.n
6
>>> isplines.lower
0.0
>>> isplines.upper
1.0

Evaluate the I-splines at some selected points:

>>> for i in range(1, isplines.n + 1):
...     print(f"I{i}: {numpy.round(isplines.I(i), 2)}")
... 
I1: [0.   0.96 1.   1.   1.   1.  ]
I2: [0.   0.52 0.84 0.98 1.   1.  ]
I3: [0.   0.09 0.3  0.66 1.   1.  ]
I4: [0.   0.   0.   0.02 0.94 1.  ]
I5: [0.   0.   0.   0.   0.58 1.  ]
I6: [0.   0.   0.   0.   0.13 1.  ]

Check that gradients are correct for Isplines.dI_dx():

>>> for i, xval in itertools.product(range(1, isplines.n + 1), x):
...     xval = numpy.array([xval])
...     def func(xval):
...         return Isplines(order, mesh, xval).I(i)
...     def dfunc(xval):
...         return Isplines(order, mesh, xval).dI_dx(i)
...     err = scipy.optimize.check_grad(func, dfunc, xval)
...     if err > 1e-5:
...         raise ValueError(f"excess err {err} for {i}, {xval}")

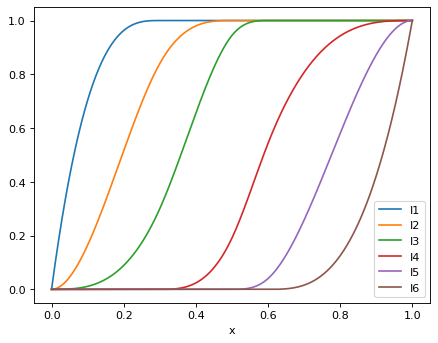
Plot the I-splines in Fig. 1 of Ramsay (1988):

>>> xplot = numpy.linspace(0, 1, 1000)
>>> isplines_xplot = Isplines(order, mesh, xplot)
>>> data = {'x': xplot}
>>> for i in range(1, isplines.n + 1):
...     data[f"I{i}"] = isplines_xplot.I(i)
>>> df = pd.DataFrame(data)
>>> _ = df.plot(x='x')

(png, hires.png, pdf)

I(i)

Evaluate spline \(I_i\) at point(s) Isplines.x.

Parameters:

i (int) – Spline member \(I_i\), where \(1 \le i \le\) Isplines.n.

Returns:

The values of the I-spline at each point in Isplines.x.

Return type:

numpy.ndarray

Note

The spline is evaluated using the formula given in the Praat manual, which corrects some errors in the formula provided by Ramsay (1988):

\[\begin{split}I_i\left(x\right) = \begin{cases} 0 & \rm{if\;} i > j, \\ 1 & \rm{if\;} i < j - k, \\ \sum_{m=i+1}^j \left(t_{m+k+1} - t_m\right) M_m\left(x \mid k + 1\right) / \left(k + 1 \right) & \rm{otherwise}, \end{cases}\end{split}\]

where \(j\) is the index such that \(t_j \le x < t_{j+1}\) (the \(\left\{t_j\right\}\) are the Msplines.knots for a M-spline of order \(k + 1\)) and \(k\) is Isplines.order.

dI_dx(i)

Derivative of Isplines.I() by Isplines.x.

Parameters:

i (int) – Same meaning as for Isplines.I().

Returns:

Derivative of I-spline with respect to Isplines.x.

Return type:

numpy.ndarray

Note

The derivative is calculated from the equation in Isplines.I():

\[\begin{split}\frac{\partial I_i\left(x\right)}{\partial x} = \begin{cases} 0 & \rm{if\;} i > j \rm{\; or \;} i < j - k, \\ \sum_{m=i+1}^j\left(t_{m+k+1} - t_m\right) \frac{\partial M_m\left(x \mid k+1\right)}{\partial x} \frac{1}{k + 1} & \rm{otherwise}. \end{cases}\end{split}\]

property j

\(j\) as defined in Isplines.I().

Type:

numpy.ndarray

property x

Points at which spline is evaluated.

Type:

numpy.ndarray

class dms_variants.ispline.Isplines_total(order, mesh, x)

Bases: object

Evaluate the weighted sum of an I-spline family (see Ramsay (1988)).

Parameters:

• order (int) – Sets Isplines_total.order.

• mesh (array-like) – Sets Isplines_total.mesh.

• x (numpy.ndarray) – Sets Isplines_total.x.

order

See Isplines.order.

Type:

int

mesh

See Isplines.mesh.

Type:

numpy.ndarray

n

See Isplines.n.

Type:

int

lower

See Isplines.lower.

Type:

float

upper

See Isplines.upper.

Type:

float

Note

Evaluates the full interpolating curve from the I-splines. When \(x\) falls within the lower \(L\) and upper \(U\) bounds of the range covered by the I-splines (\(L \le x \le U\)), then this curve is defined as:

\[I_{\rm{total}}\left(x\right) = w_{\rm{lower}} + \sum_i w_i I_i\left(x\right).\]

When \(x\) is outside the range of the mesh covered by the splines, the values are linearly extrapolated from first derivative at the bounds. Specifically, if \(x < L\) then:

\[I_{\rm{total}}\left(x\right) = I_{\rm{total}}\left(L\right) + \left(x - L\right) \left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=L},\]

and if \(x > U\) then:

\[I_{\rm{total}}\left(x\right) = I_{\rm{total}}\left(U\right) + \left(x - U\right) \left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=U}.\]

Note also that:

\[\begin{split}I_{\rm{total}}\left(L\right) &=& w_{\rm{lower}}, \\ I_{\rm{total}}\left(U\right) &=& w_{\rm{lower}} + \sum_i w_i\end{split}\]

Example

Short examples to demonstrate and test Isplines_total:

>>> import itertools
>>> import numpy
>>> import pandas as pd
>>> import scipy.optimize
>>> from dms_variants.ispline import Isplines_total

>>> order = 3
>>> mesh = [0.0, 0.3, 0.5, 0.6, 1.0]
>>> x = numpy.array([0, 0.2, 0.3, 0.4, 0.8, 0.99999])
>>> isplines_total = Isplines_total(order, mesh, x)
>>> weights = numpy.array([1.2, 2, 1.2, 1.2, 3, 0]) / 6
>>> numpy.round(isplines_total.Itotal(weights, w_lower=0), 2)
array([0.  , 0.38, 0.54, 0.66, 1.21, 1.43])

Now calculate using some points that require linear extrapolation outside the mesh and also have a nonzero w_lower:

>>> x2 = numpy.array([-0.5, -0.25, 0, 0.01, 1.0, 1.5])
>>> isplines_total2 = Isplines_total(order, mesh, x2)
>>> numpy.round(isplines_total2.Itotal(weights, w_lower=1), 3)
array([0.   , 0.5  , 1.   , 1.02 , 2.433, 2.433])

Test Isplines_total.dItotal_dx():

>>> x_deriv = numpy.array([-0.5, -0.25, 0, 0.01, 0.5, 0.7, 1.0, 1.5])
>>> for xval in x_deriv:
...     xval = numpy.array([xval])
...     def func(xval):
...         return Isplines_total(order, mesh, xval).Itotal(weights, 0)
...     def dfunc(xval):
...         return Isplines_total(order, mesh, xval).dItotal_dx(weights)
...     err = scipy.optimize.check_grad(func, dfunc, xval)
...     if err > 1e-5:
...         raise ValueError(f"excess err {err} for {xval}")

>>> (isplines_total.dItotal_dw_lower() == numpy.ones(x.shape)).all()
True

Test Isplines_total.dItotal_dweights():

>>> isplines_total3 = Isplines_total(order, mesh, x_deriv)
>>> wl = 1.5
>>> (isplines_total3.dItotal_dweights(weights, wl).shape ==
...  (len(x_deriv), len(weights)))
True
>>> weightslist = list(weights)
>>> for ix, iw in itertools.product(range(len(x_deriv)),
...                                 range(len(weights))):
...     w = numpy.array([weightslist[iw]])
...     def func(w):
...         iweights = numpy.array(weightslist[: iw] +
...                                list(w) +
...                                weightslist[iw + 1:])
...         return isplines_total3.Itotal(iweights, wl)[ix]
...     def dfunc(w):
...         iweights = numpy.array(weightslist[: iw] +
...                                list(w) +
...                                weightslist[iw + 1:])
...         return isplines_total3.dItotal_dweights(iweights, wl)[ix,
...                                                               iw]
...     err = scipy.optimize.check_grad(func, dfunc, w)
...     if err > 1e-6:
...         raise ValueError(f"excess err {err} for {ix, iw}")

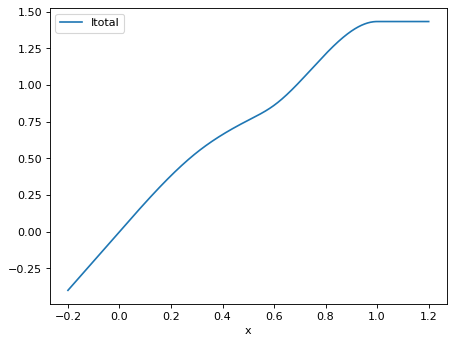
Plot the total of the I-spline family shown in Fig. 1 of Ramsay (1988), adding some linear extrapolation outside the mesh range:

>>> xplot = numpy.linspace(-0.2, 1.2, 1000)
>>> isplines_totalplot = Isplines_total(order, mesh, xplot)
>>> df = pd.DataFrame({'x': xplot,
...                    'Itotal': isplines_totalplot.Itotal(weights, 0)})
>>> _ = df.plot(x='x', y='Itotal')

(png, hires.png, pdf)

Itotal(weights, w_lower)

Weighted sum of spline family at points Isplines_total.x.

Parameters:

• weights (array-like) – Nonnegative weights \(w_i\) of members \(I_i\) of spline family, should be of length equal to Isplines.n.

• w_lower (float) – The value at the lower bound \(L\) of the spline range, \(w_{\rm{lower}}\).

Returns:

\(I_{\rm{total}}\) for each point in Isplines_total.x.

Return type:

numpy.ndarray

dItotal_dw_lower()

Deriv of Isplines_total.Itotal() by \(w_{\rm{lower}}\).

Returns:

\(\frac{\partial{I_{\rm{total}}}}{\partial w_{\rm{lower}}}\), which is just one for all Isplines_total.x.

Return type:

numpy.ndarray

dItotal_dweights(weights, w_lower)

Derivative of Isplines_total.Itotal() by \(w_i\).

Parameters:

• weights (array-like) – Same meaning as for Isplines.Itotal().

• w_lower (float) – Same meaning as for Isplines.Itotal().

Returns:

Array is of shape (len(x), len(weights)), and element ix, iweight gives derivative with respect to weight weights[iweight] at element [ix] of Isplines_total.x.

Return type:

numpy.ndarray

Note

The derivative is:

\[\begin{split}\frac{\partial I_{\rm{total}}\left(x\right)}{\partial w_i} = \begin{cases} I_i\left(x\right) & \rm{if\;} L \le x \le U, \\ I_i\left(L\right) + \left(x-L\right) \left.\frac{\partial I_i\left(y\right)}{\partial y}\right\vert_{y=L} & \rm{if\;} x < L, \\ I_i\left(U\right) + \left(x-U\right) \left.\frac{\partial I_i\left(y\right)}{\partial y}\right\vert_{y=U} & \rm{if\;} x > U. \end{cases}\end{split}\]

Note that:

\[\begin{split}I_i\left(L\right) &=& 0 \\ I_i\left(U\right) &=& 1.\end{split}\]

dItotal_dx(weights)

Deriv Isplines_total.Itotal() by Isplines_total.x.

Note

Derivatives calculated from equations in Isplines_total.Itotal():

\[\begin{split}\frac{\partial I_{\rm{total}}\left(x\right)}{\partial x} = \begin{cases} \sum_i w_i \frac{\partial I_i\left(x\right)}{\partial x} & \rm{if\;} L \le x \le U, \\ \left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=L} & \rm{if\;} x < L, \\ \left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=U} & \rm{otherwise}. \end{cases}\end{split}\]

Note that

\[\begin{split}\left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=L} &=& \sum_i w_i \left.\frac{\partial I_i\left(y\right)}{\partial y} \right\rvert_{y=L} \\ \left.\frac{\partial I_{\rm{total}}\left(y\right)} {\partial y}\right\rvert_{y=U} &=& \sum_i w_i \left.\frac{\partial I_i\left(y\right)}{\partial y} \right\rvert_{y=U}\end{split}\]

Parameters:

weights (array-like) – Same meaning as for Isplines_total.Itotal().

Returns:

Derivative \(\frac{\partial I_{\rm{total}}}{\partial x}\) for each point in Isplines_total.x.

Return type:

numpy.ndarray

property x

Points at which spline is evaluated.

Type:

numpy.ndarray

class dms_variants.ispline.Msplines(order, mesh, x)

Bases: object

Implements M-splines (see Ramsay (1988)).

Parameters:

• order (int) – Sets Msplines.order.

• mesh (array-like) – Sets Msplines.mesh.

• x (numpy.ndarray) – Sets Msplines.x.

order

Order of spline, \(k\) in notation of Ramsay (1988). Polynomials are of degree \(k - 1\).

Type:

int

mesh

Mesh sequence, \(\xi_1 < \ldots < \xi_q\) in the notation of Ramsay (1988). This class implements fixed mesh sequences.

Type:

numpy.ndarray

n

Number of members in spline, denoted as \(n\) in Ramsay (1988). Related to number of points \(q\) in the mesh and the order \(k\) by \(n = q - 2 + k\).

Type:

int

knots

The knot sequence, \(t_1, \ldots, t_{n + k}\) in the notation of Ramsay (1988).

Type:

numpy.ndarray

lower

Lower end of interval spanned by the splines (first point in mesh).

Type:

float

upper

Upper end of interval spanned by the splines (last point in mesh).

Type:

float

Note

The methods of this class cache their results and return immutable numpy arrays. Do not make those arrays mutable and change their values as this will lead to invalid caching.

Example

Demonstrate and test Msplines:

>>> import functools
>>> import itertools
>>> import numpy
>>> import pandas as pd
>>> import scipy.optimize
>>> from dms_variants.ispline import Msplines

>>> order = 3
>>> mesh = [0.0, 0.3, 0.5, 0.6, 1.0]
>>> x = numpy.array([0, 0.2, 0.3, 0.4, 0.8, 0.99999])
>>> msplines = Msplines(order, mesh, x)
>>> msplines.order
3
>>> msplines.mesh
array([0. , 0.3, 0.5, 0.6, 1. ])
>>> msplines.n
6
>>> msplines.knots
array([0. , 0. , 0. , 0.3, 0.5, 0.6, 1. , 1. , 1. ])
>>> msplines.lower
0.0
>>> msplines.upper
1.0

Evaluate the M-splines at some selected points:

>>> for i in range(1, msplines.n + 1):
...     print(f"M{i}: {numpy.round(msplines.M(i), 2)}")
... 
M1: [10. 1.11 0.  0.   0.   0.  ]
M2: [0.  3.73 2.4 0.6  0.   0.  ]
M3: [0.  1.33 3.  3.67 0.   0.  ]
M4: [0.  0.   0.  0.71 0.86 0.  ]
M5: [0.  0.   0.  0.   3.3  0.  ]
M6: [0.  0.   0.  0.   1.88 7.5 ]

Check that the gradients are correct:

>>> for i, xval in itertools.product(range(1, msplines.n + 1), x):
...     xval = numpy.array([xval])
...     def func(xval):
...         return Msplines(order, mesh, xval).M(i)
...     def dfunc(xval):
...         return Msplines(order, mesh, xval).dM_dx(i)
...     err = scipy.optimize.check_grad(func, dfunc, xval)
...     if err > 1e-5:
...         raise ValueError(f"excess err {err} for {i}, {xval}")

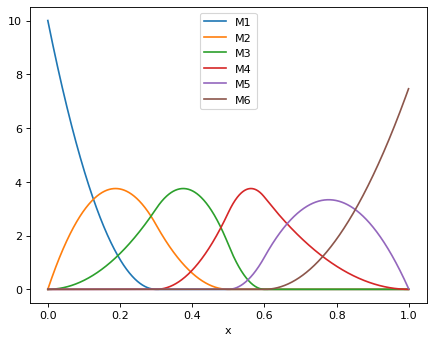
Plot the M-splines in in Fig. 1 of Ramsay (1988):

>>> xplot = numpy.linspace(0, 1, 1000, endpoint=False)
>>> msplines_plot = Msplines(order, mesh, xplot)
>>> data = {'x': xplot}
>>> for i in range(1, msplines_plot.n + 1):
...     data[f"M{i}"] = msplines_plot.M(i)
>>> df = pd.DataFrame(data)
>>> _ = df.plot(x='x')

(png, hires.png, pdf)

M(i, k=None, invalid_i='raise')

Evaluate spline \(M_i\) at point(s) Msplines.x.

Parameters:

• i (int) – Spline member \(M_i\), where \(1 \le i \le\) Msplines.n.

• k (int or None) – Order of spline. If None, assumed to be Msplines.order.

• invalid_i ({'raise', 'zero'}) – If i is invalid, do we raise an error or return 0?

Returns:

The values of the M-spline at each point in Msplines.x.

Return type:

numpy.ndarray

Note

The spline is evaluated using the recursive relationship given by Ramsay (1988):

\[\begin{split}M_i\left(x \mid k=1\right) &=& \begin{cases} 1 / \left(t_{i+1} - t_i\right), & \rm{if\;} t_i \le x < t_{i+1} \\ 0, & \rm{otherwise} \end{cases} \\ M_i\left(x \mid k > 1\right) &=& \begin{cases} \frac{k\left[\left(x - t_i\right) M_i\left(x \mid k-1\right) + \left(t_{i+k} -x\right) M_{i+1}\left(x \mid k-1\right) \right]} {\left(k - 1\right)\left(t_{i + k} - t_i\right)}, & \rm{if\;} t_i \le x < t_{i+k} \\ 0, & \rm{otherwise} \end{cases}\end{split}\]

dM_dx(i, k=None, invalid_i='raise')

Derivative of Msplines.M() by to Msplines.x.

Parameters:

• i (int) – Same as for Msplines.M().

• k (int or None) – Same as for Msplines.M().

• invalid_i ({'raise', 'zero'}) – Same as for Msplines.M().

Returns:

Derivative of M-spline with respect to Msplines.x.

Return type:

numpy.ndarray

Note

The derivative is calculated from the equation in Msplines.M():

\[\begin{split}\frac{\partial M_i\left(x \mid k=1\right)}{\partial x} &=& 0 \\ \frac{\partial M_i\left(x \mid k > 1\right)}{\partial x} &=& \begin{cases} \frac{k\left[\left(x - t_i\right) \frac{\partial M_i\left(x \mid k-1\right)}{\partial x} + M_i\left(x \mid k-1\right) + \left(t_{i+k} -x\right) \frac{\partial M_{i+1}\left(x \mid k-1\right)} {\partial x} - M_{i+1}\left(x \mid k-1\right) \right]} {\left(k - 1\right)\left(t_{i + k} - t_i\right)}, & \rm{if\;} t_i \le x < t_{i+1} \\ 0, & \rm{otherwise} \end{cases}\end{split}\]

property x

Points at which spline is evaluated.

Type:

numpy.ndarray